使用Xgboost很长时间了,虽然看过几遍原版的论文,但是对于许多的细节处理及核心公式推导一直处于比较模糊的状态,最近正好梳理了一下,希望能够把xgboost的细节表达得清楚一些。
Xgboost总结
一、Xgboost与其他树模型的联系和区别
| Xgboost | Gbdt | Adaboost | randon forest | |
|---|---|---|---|---|
| 流派 | Boosting | Boosting | Boosting | Bagging |
| 树与树的关联 | 串行,学习残差,是Gbdt在工程上的一种实现方式 | 串行,学习残差 | 串行,注重错误样本 | 并行,独立 |
| 重要性质 | 使用了目标函数的二阶泰勒展开,loss function能够二阶求导就能够进行boosting,loss function可以是很多种函数 |
二、Xgboost的数学原理
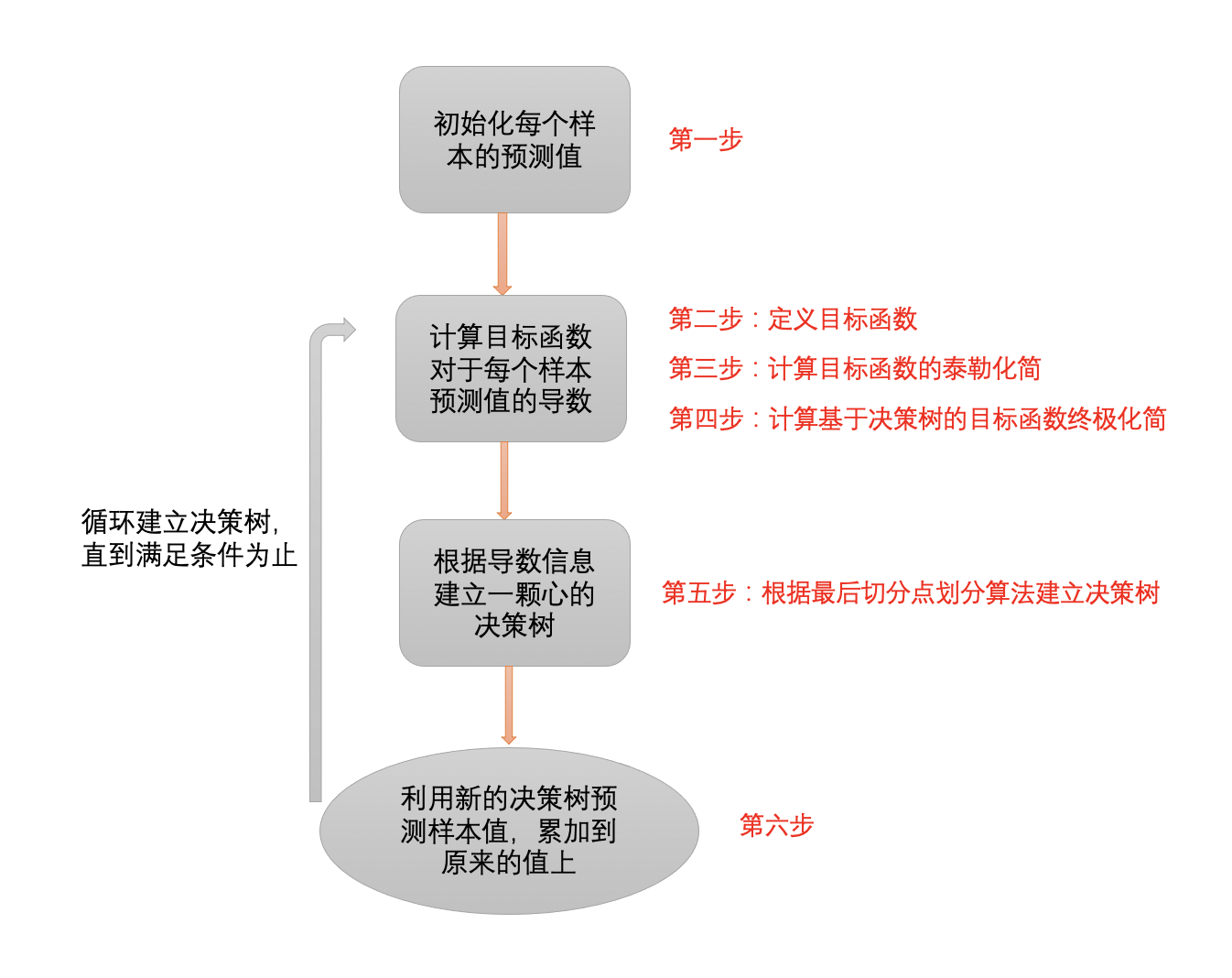
1、定义目标函数
目标函数由损失函数$L$与抑制模型复杂度的正则项$\Omega$组成:
$Obj = \sum_{i=1}^{n}l(\hat{y_i},y_i)+\sum_{t=1}^{k}\Omega(f_t)$——(1)
$n$表示样本数量,$l(\hat{y_i},y_i)$表示第$i$个样本的预测值和真实值的偏差,正则化项$\Omega(f_t) = \gamma T_{t}+\frac{1}{2}\lambda\sum_{j=1}^{T}w_{j}^{2}$,$T_t表示第$$t$棵树的叶子个数,$\sum_{j=1}^{T}w_{j}^{2}$表示所有叶子权重的平方和,$\gamma和\lambda$是超参数,$k$表示一共有$k$棵树。需注意正则化项只是用来在每次迭代中抑制弱分类器$f_i(x)$过拟合,不参与最终模型的集成。
因为Xgboost模型预测值是由所有树的预测值相加共同决定,因此以第$t$步(第$t$棵树)模型为例,模型对第$i$个样本$x_i$的预测为:$\hat y_i^t = \hat y_{i}^{t-1}+f_t(x_i)$,其中,$\hat y_{i}^{t-1}$是第$t-1$步的模型给出的预测值,是已知常数,$f_t(x_i)$是我们需要创建的新模型,所以把$\hat y_i^t$代入(1)式,可化简为:
$Obj^{t} = \sum_{i=1}^{n}l(\hat{y_i}^{t},y_i)+\sum_{i=1}^{t}\Omega(f_i)=\sum_{i=1}^{n}l(\hat{y_i}^{t-1}+f_{t}(x_i),y_i)+\sum_{i=1}^{t}\Omega(f_i)$——(2)
为了优化目标函数(2),其实相当于求解当前的$f_{t}(x_i)$,$f_{t}(x_i)$其实就是需要求解的新树
在公式(2)中,我们把$\hat{y_i}^{t-1}$视为$x$,$f_{t}(x_i)$视为$ \Delta (x)$,那么整个目标函数可以看作$F(x+\Delta x)$
联想到泰勒公式的二阶展开:$f(x+\Delta x) \approx f(x)+f’(x)\Delta x+\frac{1}{2}f’’(x)\Delta x^2$,代入公式(2)可得:
${Obj^{t} = \sum_{i=1}^{n}l(\hat{y_i}^{t-1}+f_{t}(x_i),y_i)+\sum_{i=1}^{t}\Omega(f_i)}$
$\approx\sum_{i=1}^{n}[l(\hat{y_i}^{t-1},y_i)+\frac{\partial l(\hat{y_i}^{t-1},y_i)}{\partial \hat y_i^{(t-1)}} f_t(x_i)+\frac{1}{2}\frac{\partial^2 l(\hat{y_i}^{t-1},y_i)}{\partial \hat y_i^{(t-1)}} f_t^2(x_i)]+\sum_{i=1}^{t}\Omega(f_i)$
其中,我们可以把一阶、二阶导师简写为:
$g_i = \frac{\partial l(\hat{y_i}^{t-1},y_i)}{\partial \hat y_i^{(t-1)}}$,$h_i = \frac{\partial^2 l(\hat{y_i}^{t-1},y_i)}{\partial \hat y_i^{(t-1)}}$
则(3)式可以简化为:
$Obj^t = \sum_{i=1}^{n}[l(\hat{y_i}^{t-1},y_i)+ g_i f_t(x_i)+ \frac{1}{2} h_i f_t^2(x_i)]+\sum_{i=1}^{t}\Omega(f_i)$ ——(4)
对于每一个样本的$g_i和h_i$其实在建第$t$棵树的时候是已知的,因为它只与$\hat y_i^{t-1}$和$y_i$有关,已平方损失函数为例:$\sum_{i=1}^{n}(y_i-(\hat y_i^{(t-1)}+f_t(x_i)))^2$,对于每个样本:
$g_i = \frac{\partial (\hat{y_i}^{t-1}-y_i)^2}{\partial \hat y_i^{(t-1)}}=2(\hat y^{(t-1)}-y_i)$,$h_i = \frac{\partial^2 (\hat{y_i}^{t-1}-y_i)^2}{\partial \hat y_i^{(t-1)}}=2$
所以,在(4)式中,在创建第$t$棵树时,$l(\hat{y_i}^{t-1},y_i)$,$g_i,h_i$都是已知的,我们的目标就是找到一个合适的$f_t (x)$,使得$Obj^t$最小。
(4)式中去掉一些常数项之后,可得:
$Obj^t \approx \sum_{i=1}^{n}[g_i f_t(x_i)+ \frac{1}{2} h_i f_t^2(x_i)]+\sum_{i=1}^{t}\Omega(f_i)$——(5)
其中$k$表示树的数量,那么现在到了最关键的部分了,如何构建一颗树$f_t(x)$——第$t$棵树,使得$Obj^t$目标函数最小呢?究竟如何用$f_t(x)$表示一棵树?
2、如何构建一棵树$f_t (x)$
$f_t (x_i)$的含义是某一个样本$x_i$,经过了决策树模型$f_t$所得到的预测值,在决策树上遍历得到的预测值,实际就是每个样本在决策树上遍历到叶子节点,每个叶子会有对应的权重(预测值),如下图:
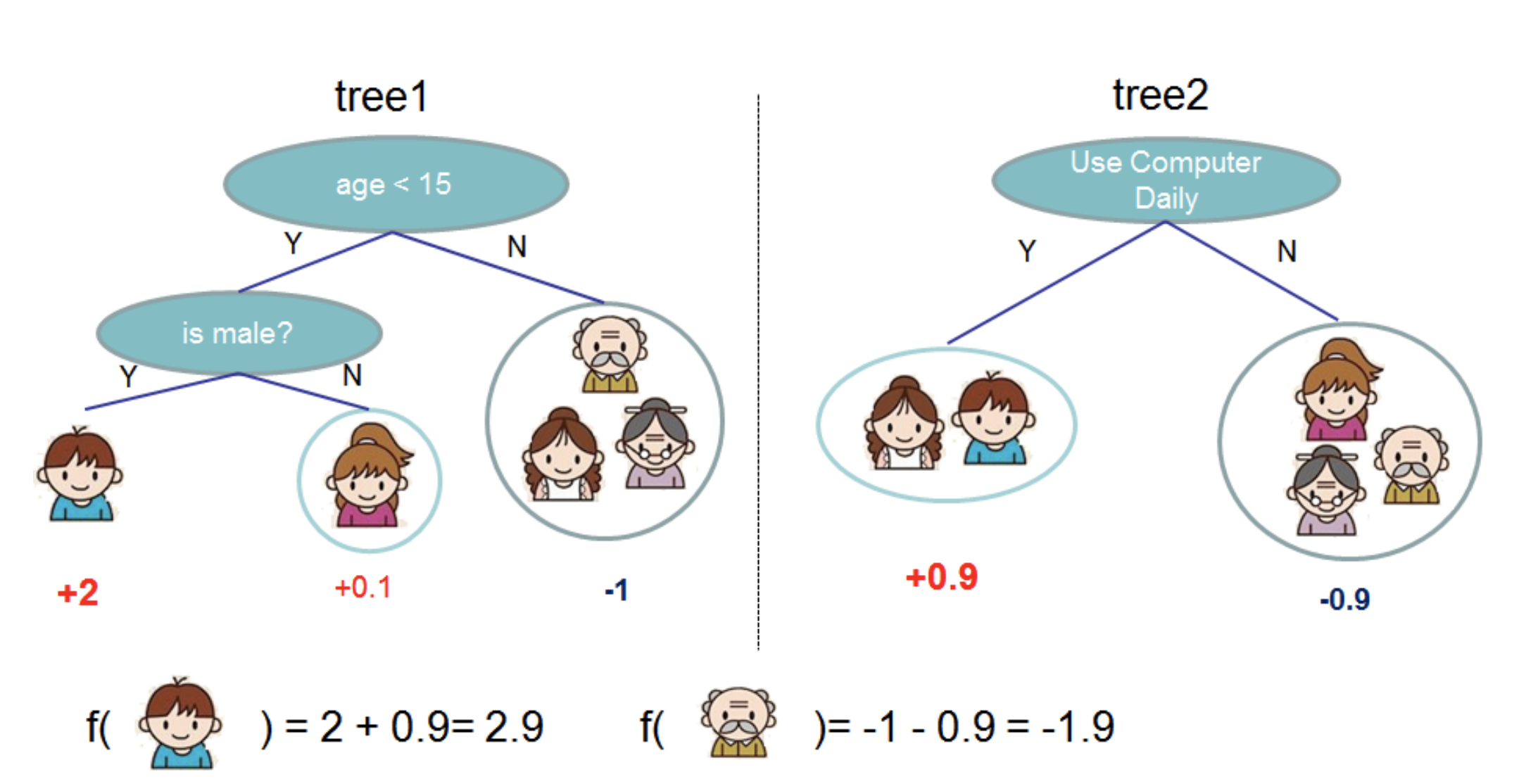
这样,我们就可以把问题进行转换,把决策树模型定义成$f_t (x)=w_{q(x)}$,其中$q(x)$代表了样本最终落在哪个叶子节点上,$w$表示该叶子节点上的权重(预测值),因此$w_{q(x)}$就代表了样本的预测值,我们可以用此定义对(5)式中的损失函数部分进行简化:
$\sum_{i=1}^{n}[g_i f_t(x_i)+ \frac{1}{2} h_i f_t^2(x_i)]=\sum_{i=1}^{n}[g_i w_{q(x_i)}+\frac{1}{2}h_i w_{q(x_i)}^2]=\sum_{j=1}^{T}[(\sum_{i\epsilon I_j} g_i) w_j+\frac{1}{2}(\sum_{i \epsilon I_j} h_i) w_j^2]$
以上,$T$表示第$t$棵树一共有多少个叶子节点,$I_j$表示一个训练样本序号集合,即表示某棵树第$j$个叶子节点上的训练样本,$w_j$为第$j$个叶子节点的取值。因此,我们使用以上简化部分的损失函数代入(5)的目标函数中,可以对目标函数进行进一步的简化:
$Obj^t \approx \sum_{i=1}^{n}[g_i f_t(x_i)+ \frac{1}{2} h_i f_t^2(x_i)]+\sum_{i=1}^{t}\Omega(f_i)$
$= \sum_{i=1}^{n}[g_i w_{q(x_i)}+ \frac{1}{2} h_i w_{q(x_i)}^2]+\Omega(f_t)$(说明:$\sum_{i=1}^{t-1}\Omega(f_i)$已经确定,因此该项为常数)
$= \sum_{i=1}^{n}[g_i w_{q(x_i)}+ \frac{1}{2} h_i w_{q(x_i)}^2]+\gamma T+\frac{1}{2} \lambda \sum_{j=1}^{T} w_j^2$
$= \sum_{j=1}^{T}[(\sum_{i\epsilon I_j} g_i) w_j+\frac{1}{2}(\sum_{i \epsilon I_j} h_i+\lambda) w_j^2]+\gamma T$
这里我们再使用$G_j=\sum_{i \epsilon I_j} g_i$ $H_j = \sum_{i \epsilon I_j}h_i$简化上式,可得:
$Obj^t=\sum_{j=1}^{T}[G_j w_j+\frac{1}{2}(H_j + \lambda)w_j^2]+\gamma T$——(6)
这里$G_j和H_j$都是由前$t-1$步就能确定的常数,只有最后一颗树的叶子节点$w_j$值不确定,目标函数可以看作是关于$w_j$的二次函数,那么将目标函数对$w_j$求一阶导数并令其等于0,可得:
$\frac{\partial J(f_t)}{\partial w_j}=G_j+(H_j+\lambda)w_j=0$,那么最终可以得到最优的$w_j^* = -\frac{G_j}{H_j+\lambda}$,一共有$T$个$w_j$参数
把最优的$w_j$代入$Obj^t$可以得到终极版本的目标函数:
$Obj^t = -\frac{1}{2}\sum_{j=1}^{T} \frac{G_j^2}{H_j+ \lambda}+\gamma T$——(7)
3、最优划分点
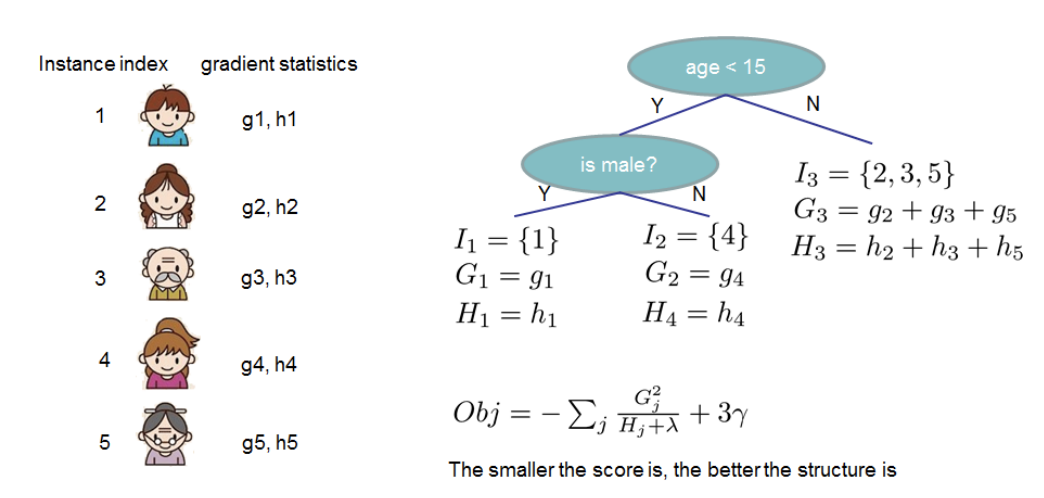
我们建立了一颗新树,每个样本都会对应到叶子节点上去,即每个样本都会对应一个$g和h$(每个样本相互独立,可以并行计算),每个叶子节点会对应$G和H$,这样就可以计算出$Obj$,而且,$g和h$的计算是不依赖与损失函数形式的,只要这个损失函数二次可微就可以了。
那么在叶子节点分裂成树的过程中最为关键的一个问题就是应该在哪个特征的哪个值上进行分裂,也就是如何寻找最优切分点的过程。
决策树在寻找最优切分点的时候需要计算一个类似收益的东西(熵增),Xgboost直接使用上面推导出的$Obj$来评估叶子节点分裂前后的$Obj$变化情况,通过$Obj$减小最多的切分点来确定最优切分点。
分裂前的目标函数可以写为:
$Obj_{pre} = -\frac{1}{2}[\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}]+\gamma$
分裂后的目标函数可以写为:
$Obj_{after} = -\frac{1}{2}[\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda}]+2\gamma$
那么分裂之后的收益为:$Gain = Obj_{pre}-Obj_{after}=\frac{1}{2}[\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda}-\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}]-\gamma$
其中$\gamma$已经考虑了树的复杂度。
有了这个$Gain$之后,我们就很容易通过遍历的方式来确定每个特征的最优划分点,然后选择收益最高的特征进行分裂(特征之间可以并行计算)。
但是对每个分割点进行计算的代价太大了了,尤其是数据量很大且分割点很多的时候,那么Xgboost采用了近似分割的方式,类似于分桶操作,一般的分桶思路是根据特征值的大小直接进行等宽或者等频的分桶,这样的方式其实是按照样本的数量进行划分,但是每个样本对$loss$的影响是不一样的,单纯按照样本数量来划分容易导致划分后左右叶子$loss$不均衡,Xgboost采用了一种对$loss$的影响权重等值百分比分位数划分算法(weight Quantile Sketch),
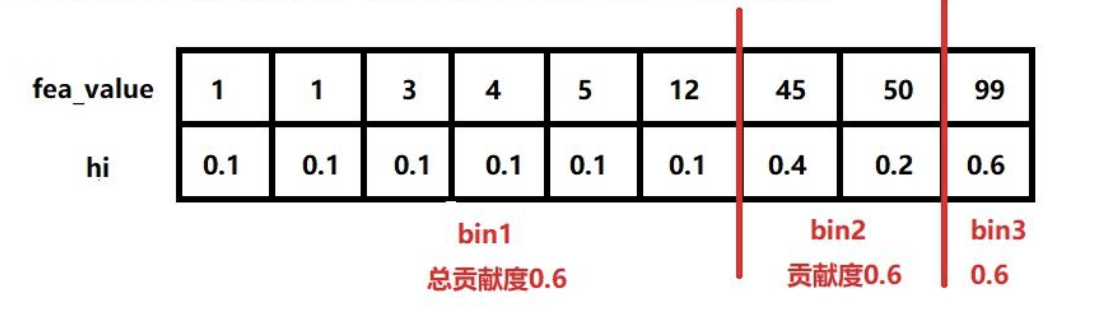
我们对上面的(4)式进行化简:
$Obj^t = \sum_{i=1}^{n}[l(\hat{y_i}^{t-1},y_i)+ g_i f_t(x_i)+ \frac{1}{2} h_i f_t^2(x_i)]+\sum_{i=1}^{t}\Omega(f_i)$ ——(4)
$=\sum_{i=1}^{n}[ g_i f_t(x_i)+ \frac{1}{2} h_i f_t^2(x_i)]+\Omega(f_t)+Constant$
$=\sum_{i=1}^{n}[\frac{1}{2} h_i \frac{2 g_i f_t(x_i)}{h_i}+ \frac{1}{2} h_i f_t^2(x_i)]+\Omega(f_t)+Constant$
$=\sum_{i=1}^{n}\frac{1}{2} h_i[2 \frac{g_i}{h_i} f_t(x_i)+f_t^2(x_i)]+\Omega(f_t)+Constant$
$=\sum_{i=1}^{n}\frac{1}{2} h_i[(2 \frac{g_i}{h_i} f_t(x_i)+f_t^2(x_i)+(\frac{g_i}{h_i})^2)-(\frac{g_i}{h_i})^2]+\Omega(f_t)+Constant$
$=\sum_{i=1}^{n} \frac{1}{2} h_i[(f_t(x_i)+\frac{g_i}{h_i})^2]+\Omega(f_t)+Constant$ #$\frac{g_i}{h_i}为常数$
$=\sum_{i=1}^{n} \frac{1}{2} h_i[(f_t(x_i)-(-\frac{g_i}{h_i}))^2]+\Omega(f_t)+Constant$ ——(8)
从这里可以看出,每棵树都是在拟合每个样本的一个残差$-\frac{g_i}{h_i}$,而$h_i$可以看做拟合某个样本残差时,这个样本的重要性,即该样本对降低$loss$的重要性权重。Xgboost引入了二阶导数之后,相当于在模型拟合降低残差的时候还给每个样本加了一个权重,而GBDT只用到了一阶导数,认为每个样本的残差对降低$loss$的贡献都是一样的。
至于按照$h_i$作为贡献度进行分桶,思路就是把所有样本的$h_i$进行累加,然后就很容易找到对应贡献度的分位点了。
整个算法构建树的过程如下所示:
以上,$\hat{y_i}^{(t-1)}$表示前$t-1$棵树的模型预测值,$f_t(x_i)$表示新加入一个新的树,$\eta$表示收缩率,目的是削弱每棵树的作用。