本章复习梳理了机器学习算法——LDA(Linear discriminant analysis)
LDA和PCA
LDA算法叫线性判别分析算法,和PCA算法类似都是压缩算法,都是求一个低维空间来近似表达高维空间从而达到压缩的目的,区别在于LDA是有监督的,PCA是最小化重构误差,使得投影后的值和原来的值尽量接近;而LDA是最大化类间距离,最小化类内距离,使得投影后的不同类别的样本分的更开而同类别的样本间更加紧密。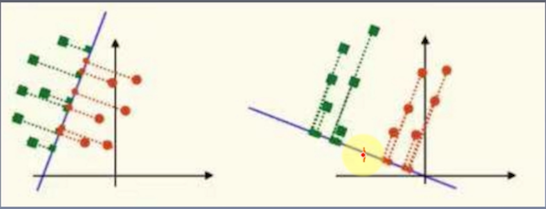
LDA的推导
设样本一共K类,每一类样本的个数为$N_1,N_2…N_k$
第1类样本为:$x_1^1,x_1^2,x_1^3…x_1^{N_1}$
第K类样本为:$x_k^1,x_k^2,x_k^3…x_k^{N_k}$
$x_i^j$变换后的样本为$\hat x_i^j = < x,u > u = (x^Tu)u$,其中$u$为投影方向上的单位向量
则第k类的类间距离即样本方差:
$S_k = \sum_{\hat x \in D_k}(\hat x - \hat m )^T (\hat x - \hat m )$,其中$\hat m$为第k类的样本均值
$= \sum [ (x^T u)u^T - (m^T u)u^T ] [ (x^T u)u - (m^T u)u ]$,其中$(x^T u),(m^T u)$为标量
$= \sum [ (x^T u)^2 u^Tu -2(x^T u)(m^T u)u^Tu+(m^T u)^2 u^Tu$,因为$u$为单位向量
$= \sum [ (x^T u)^2 -2(x^T u)(m^T u)+(m^T u)^2$
第k类的平均样本方差:
$\frac{S_k}{N_k} = \frac{\sum (x^T u)^2}{N_k} - 2 \frac{\sum x^T (um_k^T u)}{N_k} +\frac{\sum (m_k^T u)^2}{N_k}$
$ = \frac{\sum (u^T xx^T u)}{N_k} - 2 \frac{\sum x^T }{N_k}(um_k^T u) +(m_k^T u)^2$,因为$\frac{\sum x^T }{N_k} = m_k^T$
$ = u^T \frac{\sum (xx^T)}{N_k} u - (m_k^T u)^2$
$ = u^T \frac{\sum (xx^T)}{N_k} u - u^Tm_km_k^Tu$
$ = u^T(\frac{\sum (xx^T)}{N_k} -m_km_k^T)u$
所有类的类内方差之和$\sum_{k} S_k = \sum_{k} u^T(\frac{\sum (xx^T)}{N_k} -m_km_k^T)u$,令$ S_w = \sum_{k} (\frac{\sum (xx^T)}{N_k} -m_km_k^T)$,则类内方差之和$=u^TS_wu$
设类$i$和类$j$的方差为:
$S_{ij} = (\hat m_i - \hat m_j)^T (\hat m_i - \hat m_j)$
$ = u^T(m_i - m_j)^T(m_i - m_j)u$
则K个类间方差之和$\sum_{i,j}S_{ij} = u^T\sum_{i,j} (m_i - m_j)^T(m_i - m_j) u$,令$S_b = \sum_{i,j} (m_i - m_j)^T(m_i - m_j)$,则类间方差之和为$u^TS_bu$
LDA的目标是最大化类间间隔同时最小化类内间隔,因此构造目标函数:
$J(u) = \frac{u^TS_bu}{u^TS_wu}$
为了使$J(u)$最大,可以假设分母为1,最大化分子,转换为条件极值问题,利用拉格朗日乘子:$L(u,\lambda) = u^TS_bu + \lambda(1 - u^TS_wu)$
最终式子:$S_bS_w^{-1}u = \lambda u$