本章复习梳理了机器学习中常用的最优化理论知识-有约束、无约束的最优化
无约束优化
梯度下降法
使得参数沿着梯度的反方向去更新,梯度的方向是函数值增长最大的方向。
例如要求函数$f(x,y) = x^2+y^2$的最小值,此时搜索空间在点$ P(x_0,y_0) $ 处,此时点$P$所在的梯度方向是$(2x_0,2y_0)$
如何证明梯度的方向是函数值增长最大的方向?
我们假设在二维空间的$P$点$(x,y)$,移动固定长度L,则新的点$P_0(x_0,y_0)=P(x+Lcos\theta,y+Lsin\theta)$
从点$P$移动到点$P_0$,移动单位长度对函数值的增量为:$\frac{f(x+Lcos\theta,y+Lsin\theta)-f(x,y)}{L}$,
我们要求一个$\theta$使得增量最大,把增量变形:$ sin\theta \frac{f(x+Lcos\theta,y+Lsin\theta)-f(x+Lcos\theta,y)}{Lsin\theta}+cos\theta \frac{f(x+Lcos\theta,y)-f(x,y)}{Lcos\theta}$
当L趋于无穷小时,上式等于$sin\theta f_y + cos\theta f_x$
设向量$l_1 = (sin\theta,cos\theta),l_2 = (f_y,f_x)$,
$(l_1 \cdot l_2)^2 = (sin\theta f_y + cos\theta f_x) ^2 = (|l_1||l_2|cos\beta)^2 <=|l_1|^2 |l_2|^2 = (sin\theta ^2 + cos\theta ^2)(f_y ^2 +f_x ^2) = (f_y ^2 +f_x ^2)$,其中$\beta$为$l_1$和$l_2$的夹角,当$\beta$取0时取得=号,因此向量$l_1$和$l_2$平行时增量最大,即$\frac{sin\theta}{cos\theta}=\frac{f_y}{f_x}$
牛顿法
解释1:每次逐步更新x,朝着使得$f(x)’ = 0$的位置更新,即$y-g(x_0) = g’(x_0)(x-x_0)$,令$y=0$,则$x = x_0-\frac{g(x_0)}{g’(x_0)}$
解释2:在某一点用二阶泰勒公式展开,$f(x) = f(x_0)+f’(x_0)(x-x_0)+\frac{f’’(x_0)}{2!}(x-x_0)^2$,意思是在某一点利用二次函数来近似替代,然后找此二次函数的极值点,二次函数极值点$x=-\frac{b}{2a}$
$x = x_0-\frac{f’(x_0)}{f’’(x_0)}$
拟牛顿法避免了计算二阶导数,利用另外一个式子近似代替二阶导数那个式子。
梯度下降法是一次收敛,牛顿法是二次收敛???
有约束的最优化问题
拉格朗日乘子
当面对有约束的最优化问题:$min_xf(x),s.t.g(x) = 0$时,我们可以使用拉格朗日乘子进行计算,原来如下图: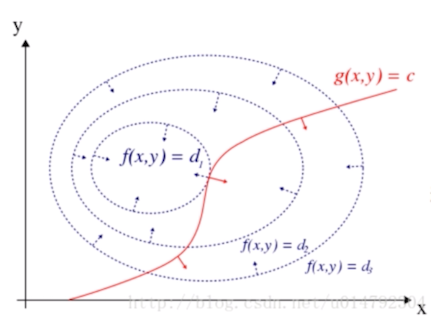
当两函数相切时取得极值点,此时满足条件:
1、两函数在相切点的法向量反向,即:$\Delta f(x) = \lambda \Delta g(x)$
2、$g(x) = 0$
因此就是拉格朗日的式子:$L(x,\lambda) = f(x) + \lambda g(x)$
如果约束条件是不等式,则称作KKT条件
$min f(x), s.t.g_i(x)>=0$
拉格朗日乘子$L = f(x) - \sum_{i}{\lambda_i}g(x_i)$
求$\frac{dL}{dx}=0, \lambda_i g(x_i)=0$