本文主要梳理了分类问题特征变量的评估指标:WOE、IV、KS;模型的评估指标AUC
WOE(weight of evidence)
对于传统的特征选择,WOE值是一个比较好的选择指标,具体的计算方法是先分箱(对于连续性变量),然后对于每个分箱,计算:$WOE_i = ln(\frac{F(p_i)}{F(n_i)}) = ln(\frac{p_i/p}{n_i/n}) = ln(\frac{p_i/n_i}{p/n})$,直观上理解就是,对于单变量的某个分箱,如果好坏比例和总体样本的好坏比例偏差太大,那么此单变量的这些取值对于目标变量的重要性相对会比较高。
IV(Information value)
IV值的定义:
$IV_i = (\frac{p_i}{p}-\frac{n_i}{n})*WOE_i$,(如果坏样本比例低于正样本的比例,WOE值为负,因此iv值还是为正)
$IV = \sum_{k=0}^{n}IV_i$
如果某变量的IV值越大,说明了此变量对于目标变量的影响越大
KS和ROC曲线
首先定义分类结果矩阵:
| 预测正 | 预测负 | |
|---|---|---|
| 真实正 | TP | FN |
| 真实负 | FP | TN |
定义:
真正例率:$\frac{TP}{TP+FN}$
假正例率:$\frac{FP}{FP+TN}$
首先把样本按照预测概率值从大到小排序,然后依次划定阈值,大于阈值的都预测为正例,然后计算累积真正例率和假正例率。
ROC曲线:横坐标为假正例率,纵坐标为真正例率
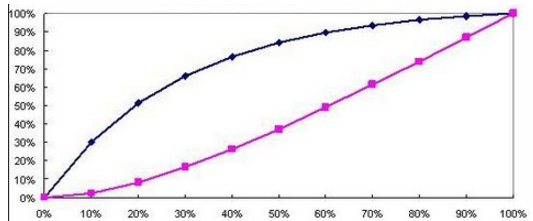
KS曲线:横坐标为划定阈值的分位数,纵坐标有两个值,一个是当前阈值下的真正例,一个是当前阈值下的假正例
AUC值:ROC曲线下的面积
KS值:MAX(真正例率-假正例率)