假设检验、T分布、T检验、F检验
T分布
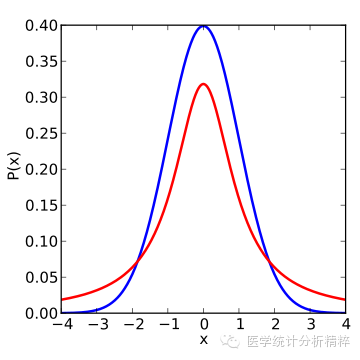
可以说,正态分布是T分布的一种特殊形式,当T分布的自由度N->无穷大的时候,T分布曲线趋于正态分布,N越小,T分布曲线越扁越宽,样本数量越小,自由度越小。
相比于正态分布,T分布更适应于小样本的假设检验,因为T分布更能够排除异常值的干扰,准确把握数据的特性(集中和离散)
假设检验
假设检验一般会先定义问题(零假设、备则假设),然后得到显著性p值,划定p值在某个范围内时,接受原假设,否则接受备则假设
第一、二类错误:当我们的零假设为真,但结论认为零假设不正确,即弃真,这是第一类错误;当零假设为假,结论认为零假设是对的,即取伪,这是第二类错误,这两类错误无法同时避免,大多数情况下,我们一般控制犯第一类错误,称之为显著性水平p,例如p<=0.05,认为犯第一类错误的概率很小,为什么控制犯第一类错误呢,原因是一般我们设定的零假设都是无效、无用、无影响等等,这时候如果把无效的事情错误的判断为有效的,那么造成的影响可能会很大,但是第二类错误的影响就相对没那么大。
T检验
T检验-student检验,是使用t分布理论来比较总体期望差异是否显著,因为小样本的差异并不能代表总体的差异,而可能是取值的问题,
T检验的操作过程:
T检验步骤
1、建立零假设 $H_{0}$:u=1.1 和备则假设 $H_1$,并限定显著性水平,比如$a$
2、选择T统计量,计算T统计量,计算公式:
其中$s$是样本的标准差
3、查看T检验临界值表,当统计量小于表值时,我们接受零假设$H_0$
F检验
F检验,比较两个正态分布的方差是否相等,即方差齐性
F检验步骤
1、设$x \thicksim N(u_1,\sigma_1^2)$,$y \thicksim N(u_2,\sigma_2^2)$建立零假设和备则假设:
$H_0:\sigma_1^2=\sigma_2^2$,显著性水平设为$p=0.1$
2、选择统计量$s=\frac{s_x^2}{s_y^2}$,其中$s_x^2$为$x$的样本方差,$s_y^2$为$y$的样本方差
3、查询F检验临界值表,当统计量小于表值时,我们接受零假设$H_0$